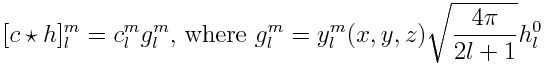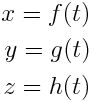Home

This is a continuation of the tutorial on spherical harmonic applications for games. On the last page, we figured out the core math for integrating a basic diffuse BRDF with a spherical environment of incident light.

Efficient implementation

So far, we've been dealing with spherical harmonics fairly abstractly. But now we can get down to a concrete use and some concrete code. Given our input texture (which effectively describes a sphere of incident light on a point) we want to calculate, for a given normal direction, what is the appropriate diffuse response.

To explain that more visually, here's the images from the first page. The first one is the input texture, and the second one is the matching diffuse response (with the same mapping).


(images from sIBL Archive: http://www.hdrlabs.com/sibl/archive.html)

Recall that we've expressed the BRDF as zonal harmonic coefficients and the incident light environment as spherical harmonic coefficients. We've established that we need to use a "convolve" operation to calculate how the BRDF reflects incident light to excident light (this effectively calculates the integral of the BRDF across the incident sphere). We also worked out that we need to rotate the BRDF in order to align it with the direction of the normal.

To refresh, here's the equation for convolution and rotation:

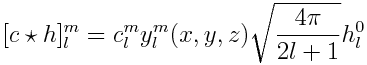
The output of the convolve operation is a set of coefficients, and our final result will be the sum of those coefficients.

Simplifying

Let's define g by rearranging the convolve equation:

More on spherical harmonics is coming, but this is a slight intermission about Vulkan. Yesterday, I got a chance to attend a Vulkan workshop (called Vulkan DevU) in Vancouver, Canada. It was a short conference with talks by some of the Vulkan working group, with a mixture of both advanced and beginner sessions. You can get the slides here.

Unfortunately, isn't been awhile since I've touched the Vulkan implementation in XLE, and it wasn't fresh in my mind -- but I got a chance to meet some of the working group members and ask a bunch of random questions. Lately it's been difficult to find enough time to properly focus on low level graphics in XLE; I've had to prioritize other things.

My impressions of Vulkan's strong points were re-affirmed by this conference. Vulkan has a fundamentally open nature and is naturally industry driven -- and working group showed a desire to become even more open; both by inviting contributions and suggesting they would change their NDA structure so they can speak about upcoming drafts sooner in the process.

Vulkan creates a practical balance between compatibility and performance; and the team addressed that directly. They also spoke about their desire to keep Vulkan thin and avoid heuristics -- another great property of the library.

So, they gave me every reason to think that Vulkan was in good hands. However, during the conversations we also started to touch upon some of the potential risks of the Vulkan concept. They were upfront about the desire to create a successor to OpenGL, which implies a very broad usage of the API (awesome!) but, in my opinion, there are some possible risks:

DirectX 12

After what seemed like an uncertain start, DX12 looks like it could be very strong. The fact that it shares many fundamental properties with Vulkan makes the two natural competitors.

Part of DirectX's strength is that is has for many years worked hand and hand with GPU hardware development. Generally important (game oriented) hardware features need to be exposed by the DX API before they are "real" -- so Nvidia, AMD & Intel must fight it out to guide the API to best suit whatever hardware feature they want to emphasize. Over the years, both Nvidia and AMD have attempted to lessen their dependence on DX (with GL extensions or Mantle, etc) but it hasn't worked so well. If you want to make a major change (eg, multicore GPUs, bindless, etc), game developers have a tendency to ignore it until it's in DX.

The problem for Vulkan is that it risks having to just trot along after DX, or becoming too bound to whichever hardware vendor that feels left out in the cold by the DX council (or, alternatively, mobile oriented hardware vendors that don't have as much skin in DirectX)

Shifting responsibilities onto engine teams

Vulkan shifts some of the responsibilities that were previously handled by GPU driver teams onto the game engine team. This is particularly obvious in areas such as memory management, scheduling and coherency... But it's a general principle, sometimes referred to as the "explicit" principle. For me, this is Vulkan's greatest attribute; but there are risks associated also.

This is a continuation of the previous page; a tutorial for using spherical harmonic methods for real time graphics. On this page we start to dig into slightly more complex math concepts -- but I'll try to keep it approachable, while still sticking to the correct concepts and terms.

Integrating the diffuse BRDF

On the previous page, we reconstructed a value from a panorama map that was compressed as a spherical harmonic. The result is a blurry version of the original panorama.

Our ultimate goal is much more exciting, though -- what if we could calculate the diffuse reflections at a material should exhibit, if it was placed within that environment?

This is the fundamental goal of "image based" real time lighting methods. The easiest way to think about it is this -- we want to treat every texel of the input texture as a separate light. Each light is a small cone light at an infinite distance. The color texture of texel tells us the color and brightness of the light (and since we're probably using a HDR input texture, we can have a broad range of brightnesses).

Effectively, the input texture represents the "incident" light on an object. We want to calculate the "excident" light -- or the light that reflects off in the direction of the eye. We're making an assumption that the lighting is coming from far away, and the object is small.

Since our input texture has a finite number of texels, we could achieve this with a large linear sum:

Where t is a texel in the input texture, I is the color in the input texture, d is the direction defined by the mapping (ie, equirectangular or cubemap), a is the solid angle of the texel, and L() is our (somewhat less than bi-directional) BRDF. In spherical harmonic form, we would have to express this equation as a integral (because the spherical harmonic form is a non-discrete function).

But we can do better than this. It might be tempting to consider the blurred spherical harmonic reconstruction of the environment as close enough -- but, again, we can do better!

Zonal harmonics

Yikes; it's been awhile since my last update!

I wanted to share a little bit of information from a technique I've recently been working on for an unrelated project. The technique uses a series of equations called "spherical harmonics" for extremely efficient high quality diffuse environment illumination.

This is a technique that started to become popular maybe around 15 years ago -- possibly because of its usefulness on low power hardware. It fell out of favour for awhile, I was never entirely clear why. I got some good value from it back then, and I hope to get more good value from the technique now; so perhaps it's time for spherical harmonic's star to come around again?

There's a fair amount of information about spherical harmonics on the internet, but some of can be a little dense. There seems to be lack of information on how to take the first few steps in applying this math to the graphics domain (for example, for diffuse environment lighting). So I'll try to keep this page approachable for graphics programmers, while also linking off to some of the more dense and abstract stuff later on. And I'll focus specifically on how I'm using this math for graphics, how I've used it in the past, and how I'd like that to grow in the future.

What are spherical harmonics

The "spherical harmonics" are a series of equations that we'll use to compress lighting information greatly. The easiest way to understand them is to start with something simpler and analogous -- and that is cubic splines.

Splines are a method of describing a curve through space with a finite number of points (or points and tangents). Even though the curve is defined by a finite number of parameters, the result is effectively an infinite number of points. To define the curve, we need equations of the form:

Where t is the distance along the spline (usually between 0 and 1) and x, y & z are cartesian coordinates. In the case of cubic splines, the functions f, h and g are cubic polynomials. If you've used Bezier splines before, you may be familiar with a way to express these polynomials using a form called a "Bernstein polynomial".

Bernstein basis

Work is still continuing on XLE! Over the last few weeks, I've have been very distracted by other priorities. I'm likely to be somewhat busy and distracted during for a few more weeks until things return to a more normal situation. However, I'm still finding time to work on XLE, and make some improvements and fixes!

Lately, my focus has been on Vulkan support (in the experimental branch). Vulkan is looking more and more stable and reliable, and the HLSL -> SPIR-V path is working really well now! However, there are still some big things I want to improve on:

• Improved interface for BoundUniforms, that can allow for precreation of descriptor sets during loading phases
• Improved interface for Metal::ConstantBuffer and temporary vertex/index buffers that would rely on a single large circular device buffer
• Pre-create graphics pipelines when using SharedStateSet (eg, when rendering RenderCore::Assets::ModelRenderer)
  • (this might also involve a better solution for the render state resolver objects used by materials)
• Fix triangle hit-test supported used by the tools (which is complicated by the render pass concept and requires stream output support)
• Tessellation support for terrain rendering
• Integration of MSAA resolve for Vulkan

With these changes, we should start to see much more efficient results with the Vulkan pipeline. Some SceneEngine features won't work immediately, but otherwise we will be getting very good Vulkan results, while also retaining the DirectX compatibility!